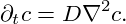
(1)

It describes the change of the local composition of a system in non-homogeneous systems like, e.g., mixtures of spatially varying concentration. Diffusion is a dynamic process driven by thermal motion of a large number of microscopic particles, which does, however, not lead to any macroscopic motion.

Looking at the equation, we see that diffusion “straightens out” the concentration profile c(X) until some linear slope compliant with the boundary conditions is reached. In an infinite (or periodic) system, this means that diffusion simply homogenizes the concentration to c(X) = const.. If you have a little knowledge of equilibrium thermodynamics, this will not come as a surprise to you, as the state with equal concentration everywhere is clearly the state of higher entropy.¹

Here, we want to take a closer look at this connection between entropy and diffusion. For starters, we will consider the simple case of an ideal gas and then move on to more realistic gases (here: the van-der-Waals gas) as well as to binary mixtures.

1 Diffusion of an ideal gas

The internal energy U and the entropy S of an ideal gas can be written in the form

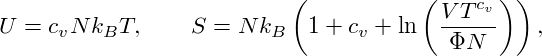(2)

with constant Φ. Thus we obtain the Helmholtz free energy A²

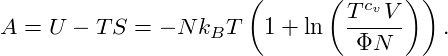(3)

From this, we obtain the chemical potential by derivation with respect to N:

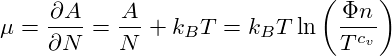(4)

with n = N∕V .

Diffusion is directly connected to the chemical potential via Teorell’s equation (see eq. (1) in [Teo35])

(5)

For an ideal gas at constant temperature, we find

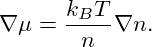(6)

And here we notice, that the factor of n⁻¹ in ∇μ will exactly cancel with the factor n in the diffusive flux. The result is simply

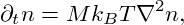(7)

so that we have obtained the diffusion equation where the diffusion constant is determined by the Einstein relation D = Mk_BT (see the equation following eq, (2) in [Ein05], where N denotes Avogadro’s constant). If we write the diffusion equation in terms of a flux J, so that

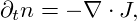(8)

we see that J = −D∇n. The statement, that the diffusive flux is proportional to the negative concentration gradient is known as Fick’s first law.

2 Diffusion of a van-der-Waals gas

The Helmholtz free energy of a van-der-Waals gas is given by

(9)

Like in the previous section, we want to calculate the gradient of the chemical potential and write it in terms of n. At constant temperature, ∇μ can calculated like

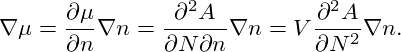(10)

Inserting the free energy from eq. (9), we find

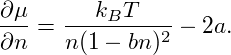(11)

Interestingly, this term can actually have both signs. It becomes negative for small enough T and n close to 1∕(3b), the maximum of the denominator. As we will show shortly, this has important consequences for the dynamics of the gas. The diffusion equation is then given by

(12)

where the coefficient of the term with ∇²n is

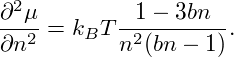(13)

This equation is basically a Cahn-Hilliard equation (see the note on first order phase transitions for more details), except that the interfacial energy of phase domain boundaries is neglected here. Just like in the case of the Cahn-Hilliard equation, homogeneous solutions n(x) = n₀ are linearly unstable, when (∂μ∕∂n)|_n=n0 is negative. This corresponds to systems within the spinodal region.

References